Хочется задавать положение объекта в пространстве однозначно. Достаточно очевидно что любое положение однозначно определяется 3 поворотами вокруг разных осей. Но встаёт вопрос в каком порядке вращать и как выбрать оси?

Обобщённую матрица поворота можно задать по разному. С одной стороны мы можем вращать объект вокруг неподвижных осей. С другой вокруг осей связанных с объектом ещё их называют локальными. Стоит вспомнить что операции умножения матриц не коммутативна поэтому для однозначного определения положения нужно знать не только 3 угла, но и схему умножения матриц.

Можно выделить 2 популярные схемы.
1) Матрица поворота через углы Эйлера.
2) Матрица поворота через углы летательного аппарата (ЛА): рыскание, тангаж и крен(yaw, pitch и roll).
В виду того что первая требует большого числа вычислений, то на практике обычно применяют вторую.

Углы Эйлера - три угла однозначно определяющие ориентацию твёрдого тела, определяющие переход от неподвижной системы координат к подвижной.
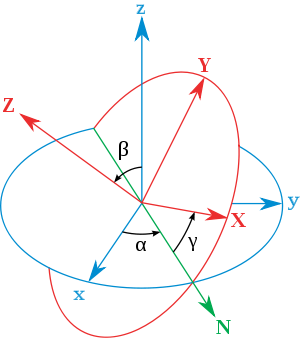
Подвижная система координат это система координат привязанная к телу. Иногда говорят в мороженная в тело. Прежде чем дать определения углов нам понадобиться ещё одно. Линия узлов ON - линия пересечение плоскости OXY и Oxy

α (или φ) это угол между осью Оx и осью ON. Диапазон значений [0, 2*Pi) - угол собственного вращения
β (или θ) это угол между осью Oz и осью OZ. Диапазон значений [0, 2*Pi) - угол нутации
γ (или ψ) это угол между осью ON и осью OX. Диапазон значений [0, Pi) - угол прецессии

[1],[2]
Отсюда виден что порядок вращения будет следующий вначале по оси Z, затем по оси X, и снова по оси Z.

Вспомним умножение матрицы на вектор. Оно используется для перехода в новую систему координат. 1.
1. <math>X_{new}=R*X </math>
2. <math>X_{new}=R_Z(\alpha)*X </math>
3. <math>X_{new}=R_X(\beta)*X </math>
4. <math>X_{new}=R_Z(\gamma)*X </math>
5. <math>X_{new}=R_Z(\gamma)*R_X(\beta)*R_Z(\alpha)*X </math>
Отсюда видно что обобщённая матрица поворота будет равна.
6. <math>R=R_Z(\gamma)*R_X(\beta)*R_Z(\alpha) </math>

Примечание здесь записаны поворот относительно подвижных осей. Что требует вычисления этих осей.

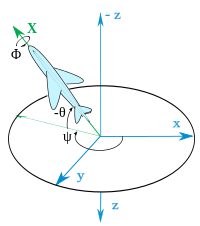
Матрица летательного аппарата(далее Матрица ЛА).
Угловое положение летательного аппарата однозначно определяется 3 углами:
рыскание(ψ), тангаж(θ) и крен(γ).

Крен - это угол между осью проходящею через крыло и местной горизонтальной плоскостью. Термин местное взялся из-за того что земля круглая и обычно оно отсчитывается от местного положения. Но в играх обычно мир является плоским.
Тангаж - это угол между осью проходящею через хвост к носу ЛА и местной горизонтальной плоскостью.
Рысканье - это угол между осью проходящею через хвост к носу ЛА и начальным направлением. В качестве начального направления принято брать ось Ox стационарной системы координат.
Более формальное определение дано в [5].

Для вывода матрицы поворота будем действовать по шагам. Вспомним уровнение умножение матрицы на вектор. Оно используется для перехода в новую систему координат. 1.
1. <math>X_{new}=R*X </math>
Затем сделаем поворот по крену. Эту легко сделать так как ось Ox совпадает с OX.
2. <math>X_{new}=R_x*X </math>
Затем повернём по тангаж. Оси Oy совпадает с OY.
3.<math>X_{new}=R_y*X </math>
Затем повернём по углу рыскания, так как у нас ось Oz совпадает с OZ.
4.<math>X_{new}=R_z*X </math>
Отсюда видно что обобщённая матрица поворота будет равна 6.
5.<math>X_{new}=R_z(roll)*R_y(pitch)*R_x(yaw)*X </math>
6.<math>R=R_z(roll)*R_y(pitch)*R_x(yaw) </math>
Как результат мы получаем очень простую формулу для матрицы ЛА

Матрица ЛА в отличии от матрицы Эйлера требует гораздо меньше вычислений. Так как в момент вращения подвижные оси совпадают со стационарными.

Список литературы:
[1] http://www.femto.com.ua/articles/part_2/4600.html
[2] http://en.wikipedia.org/wiki/Roll-pitch-yaw#Tait.E2.80.93Bryan_angles
[3] http://msdn.microsoft.com/en-us/library/windows/desktop/bb205361(v=vs.85).aspx
[4] http://www.gamedev.ru/code/articles/faq_matrix_quat
[5] http://window.edu.ru/resource/324/45324/files/dstu27.pdf
[6] http://www.youtube.com/watch?v=tRrydagL2aw