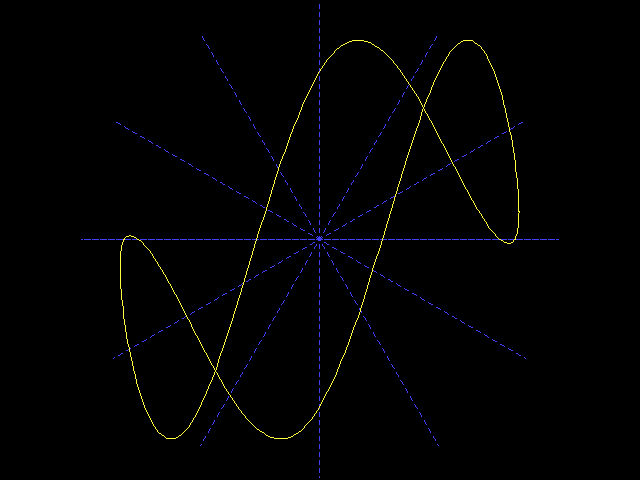Содержание
Построение графика функции
Системы координат
Пусть график вида y = f(x) должен размещаться на поверхности холста с размерами CanvasWidth (ширина) на CanvasHeight (высота) пикселей.
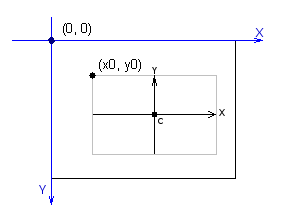
Центр координат находится в левом верхнем углу экрана. Ось X направлена вправо, как принято, а ось Y направлена вниз. Определим прямоугольную область (холста), в которой будем выводить график. Левый верхний угол холста определяется координатами (X0, Y0) в системе координат экрана.
Мы разместим центр коодинат нашей системы координат в центре холста. По этой причине необходимо задать величины Cx, Cy для смещения его в центр экрана (представляющую из себя матрицу пикселов). Cx и Cy определяются так:
Cx := CanvasWidth DIV 2; Cy := CanvasHeight DIV 2;
Так как параметры у функции вещественного типа, а для отображения на экране необходимо задавать целочисленные значения, то необходимо округлять значения. Это можно сделать функцией Round().
Масштабирование
Перед построением графика надо:
- Определить граничные значения входных параметров (ось X):
a,b.
Эти параметры задаются пользователем и именно в этом интервале стоится заданная функция. - Найти коэффициент масштабирования данных по формуле:
K = CanvasWidth / (b - a)
Итак, для отображения каждой точки функции мы учитываем коэффициенты для их масштабирования (умещения) на экране по следующим формулам:
по оси X: px := x0 + Cx + Round( x * K )
по оси Y: py := y0 - Cy - Round( y * K )
{ Функция преобразования в координату X пиксела } FUNCTION PixelCoordX (xx: Double): Integer; BEGIN { прибавляем половину ширины холста, чтобы центр осей был в центре экрана } Result := x0 + Cx + Round( xx * K) END; { Функция преобразования в координату Y пиксела } FUNCTION PixelCoordY (yy: Double): Integer; BEGIN { вычитаем из половины высоты холста, иначе график будет перевёрнутым } Result := y0 + Cy - Round( yy * K ) END;
Табуляция функции
А теперь про то какие значения функции берутся.
Функцию f(x) выводят, используя табуляцию. Иными словами, необходимо изначально задать шаг табуляции значений x. Назовём этот шаг константой deltaX. Обычно за deltaX принимают доли от единицы (сотые, тысячные и т.д.). Допустим, deltaX = 0.01 . Это и есть точность табуляции функции. Если эту величину выбрать достаточно большой, то при построении функции график будет состоять не из плавных, а ломаных линий.
График функции выводят, начиная от наименьшего значения x до наибольшего. Переменная x будет принимать значения, начиная от a и заканчивая b, прибавляясь с каждым остчётом на константу deltaX, пока не достигнет наибольшего значения b.
Выражая это на языке Паскаль (отрывок из кода программы),
{ подсчёт коэффициента масштабирования } K := 1.0 * CanvasWidth / (b - a); x := a; y := f(x); px := PixelCoordX(x); py := PixelCoordY(y); MoveTo(px, py); WHILE x <= b DO BEGIN y := f(x); px := PixelCoordX(x); py := PixelCoordY(y); { проводим линию до заданной точки от установленного ранее курсора (процедурами MoveTo/LineTo) } LineTo(px, py); x := x + deltaX END;
Примеры
В декартовой С.К.
Итак, пример для Free Pascal:
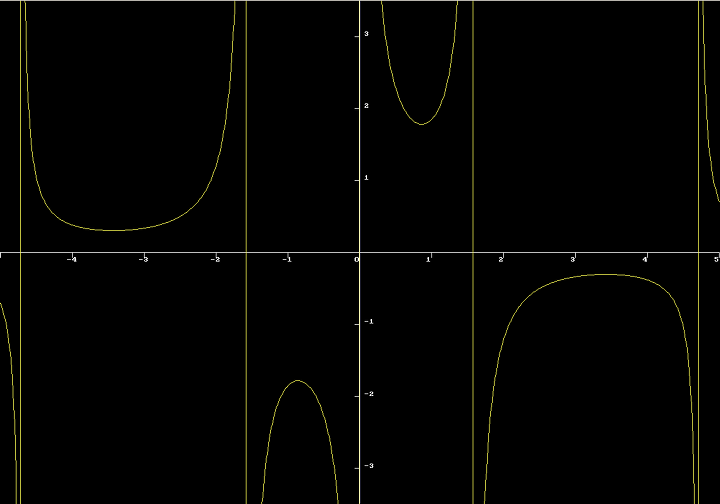
{$MODE ObjFpc} USES Graph, SysUtils; CONST deltaX = 0.01; { шаг табуляции функции } Inf = 3.4e38; { +infinity, NAN } { задание функции формулой } FUNCTION Func (x: Double): Double; BEGIN {Result := 2.2} {Result := 2*x*(x-3) * sqr(abs(x) - sin(x))} IF (x <> 0) And (x <> pi/2) THEN Result := 1 / (x * cos (x)) ELSE Result := Inf { бесконечность } END; PROCEDURE PlotGraph (x0, y0, CanvasWidth, CanvasHeight: Integer; a, b: Double); VAR K: Double; {коэффициент масштабирования графика } Cx, Cy: Integer; { половины ширины и высоты холста } { Функция преобразования в координату X пиксела } FUNCTION PixelCoordX (xx: Double): Integer; BEGIN { прибавляем половину ширины холста, чтобы центр осей был в центре экрана } Result := x0 + Cx + Round( xx * K) END; { Функция преобразования в координату Y пиксела } FUNCTION PixelCoordY (yy: Double): Integer; BEGIN { вычитаем из половины высоты холста, иначе график будет перевёрнутым } Result := y0 + Cy - Round( yy * K ) END; { построение осей координат } PROCEDURE PlotAxes; CONST h = 0.2 / 3.0; VAR r: Double; BEGIN { Строим ось X } Line(x0, y0 + Cy, x0 + CanvasWidth - 1, y0 + Cy); { Строим ось Y } Line(x0 + Cx, y0, x0 + Cx, y0 + CanvasHeight - 1); r := Trunc(a); WHILE r <= Trunc(b) DO BEGIN { метки на шкале X } Line(PixelCoordX (r), PixelCoordY (0), PixelCoordX (r), PixelCoordY (-h)); { числа на шкале X } OutTextXY(PixelCoordX (r - h), PixelCoordY (-h), IntToStr(Round(r))); { метки на шкале Y } Line(PixelCoordX (0), PixelCoordY (r), PixelCoordX (-h), PixelCoordY (r)); { числа на шкале Y } IF r <> 0 THEN OutTextXY(PixelCoordX (h), PixelCoordY (r + h), IntToStr(Round(r))); r := r + 1.0; END; END; VAR x, y: Double; px, py: Integer; BEGIN IF b <= a THEN Exit; Cx := CanvasWidth DIV 2; Cy := CanvasHeight DIV 2; { подсчёт коэффициента масштабирования } K := 1.0 * CanvasWidth / (b - a); { построение осей координат } PlotAxes; { построение графика } SetColor(Yellow); x := a; y := Func(x); px := PixelCoordX(x); py := PixelCoordY(y); MoveTo(px, py); WHILE x <= b DO BEGIN y := Func(x); px := PixelCoordX(x); py := PixelCoordY(y); { проводим линию до заданной точки от установленного ранее курсора (процедурами MoveTo/LineTo) } IF y < Inf THEN LineTo (px, py); x := x + deltaX END; END; VAR gd, gm: smallint; BEGIN gd:=Detect; gm:=0; InitGraph(gd, gm, ''); IF GraphResult <> grOK THEN Exit; PlotGraph (0, 0, GetMaxX(), GetMaxY(), -5.0, 5.0); readln; CloseGraph END.
Это был пример для вывода графика в декартовой системе координат (С.К.).
Теперь рассмотрим другие С.К.