Операция умножения матрицы на вектор.
Операция умножения определяется как умножение каждой строки матрицы на вектор(вектор-столбец). Где умножение строки описывается как формула скалярного произведения.
Результат записывается в вектор с элементом равным строке.
Схематически это показано на рисунке.
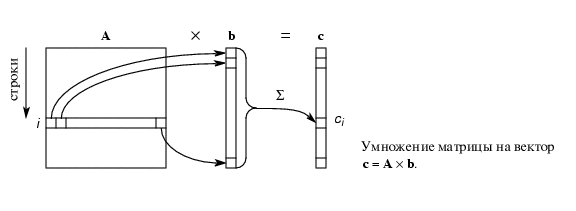
Рисунок 1.
Формальная запись.
1. <math>c_{i} = \sum^n_{j=1} a_{ij} \cdot b_{j} </math>
Где:
i - номер строки матрицы А, принимает значения от 1 до m; j - номер столбца матрицы A, принимает значения от 1 до n; m - число строк в матрице А; n - число столбцов в матрице А.
Число элементов в векторе b должно быть равно число столбцов в матрице.
Алгоритм умножения матрицы на вектор
procedure Mul_Base(var R:TVectorN; A:TMatrixNM; B:TVectorN); var i,j:Integer; Tmp:Real; begin for i:=0 to RowsCount(A)-1 do begin Tmp:=0; for j:=0 to ColumnsCount(A)-1 do Tmp:=Tmp+A[i,j]*B[j]; R[i]:=Tmp; end; end;
Входные параметры:
- Прямоугольная матрица A.
- Вектор B.
Выходные параметры:
- Прямоугольная матрица R.
Примечание:
- Входные параметры не проверяются. Память под вектор R должна быть выделена. Вектор R должен иметь число элементов равное числу строк матрицы A. Вектор B должен иметь число элементов равное числу столбцов матрицы A.